閱讀以下材料����,回答下列問題.
材料一 淮河流域自古是我國農業(yè)發(fā)達的地區(qū),可現(xiàn)在卻成為水旱災害多發(fā)的地區(qū).當?shù)匾磺裰{唱出了淮河的滄桑:“50年代淘米洗菜���,60年代洗衣灌溉�,70年代水質變壞�����,80年代魚蝦絕代”.
材料二 我國每年耕地表土凈流失量高達262平方千米.而且荒漠化面積仍以較快速度擴展.2001年春季,我國東北���、華北���、西北地區(qū)發(fā)生多次揚沙、沙塵暴天氣���,導致北京空氣污染嚴重�����,迫使機場、公路交通無法正常運行�,影響正常經(jīng)濟發(fā)展和人民日常生活.早在1991年北京就被內羅畢國際會議列為“沙漠化邊緣城市”.
材料三 隨著我國北方人口的劇增,無節(jié)制地抽取地下水���,導致地下水位大幅下降���,有些地區(qū)地下水埋深已經(jīng)低于植物根系分布的深度,結果造成植物枯死���,土地失去植被保護���,極易起沙塵暴.
(1)現(xiàn)在����,我國的環(huán)境問題比較嚴重���,主要表現(xiàn)在______和______兩個方面.
(2)人類與環(huán)境的關系是在______和______活動中發(fā)生的.
(3)近些年來����,北京經(jīng)常遭受沙塵暴的影響���,原因之一就是位于強勁的______風的下風向.
(4)我國北京的沙塵暴可以治理和預防�����,下列措施有助于沙塵暴治理的是______.
①在大面積露天采礦的棄土上種草
②建設“三北”防護林
③增加海洋水汽到達陸地的數(shù)量
④采取人工措施�����,大面積加快高山冰川融化
⑤禁止山區(qū)毀林開荒���、草原毀草開荒
A.①②③④B.③④⑤C.②③⑤D.①②⑤
(5)近年來,我國近海多次發(fā)生赤潮����,其主要原因是______.
A.洋流改變了熱量平衡
B.厄爾尼諾引起氣候異常
C.人類活動向海洋排放污染物�,導致海水富營養(yǎng)化
D.魚類減少使海洋空間增加�����,引起藻類過度生長.

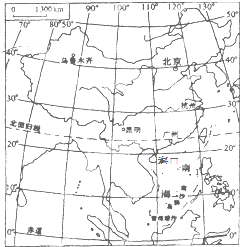 讀中國地圖,回答下列問題:
讀中國地圖,回答下列問題: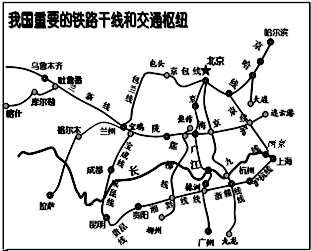 讀交通圖完成下列各題:
讀交通圖完成下列各題: