(1) 水平拉力F的大小;(2) 在t=10s末立即撤去F,物體還能運動多遠? 【查看更多】

 

題目列表(包括答案和解析)

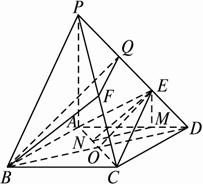
底面是菱形的四棱錐P—ABCD中,∠ABC=60°,PA=AC=a,PA⊥平面ABCD,點E在PD上,且PE∶ED=2∶1.

(1)求二面角EACD的?大小?.

(2)在棱PC上是否存在一點F,使BF∥平面AEC?若存在,求出點F;若不存在,請說明理由.

查看答案和解析>>

以O為原點，
OF
所在直線為x軸，建立直角坐標系．設
OF
•
FG
=1，點F的坐標為（t，0），t∈[3，+∞）．點G的坐標為（x0，y0）．
（1）求x0關于t的函數(shù)x0=f（t）的表達式，并判斷函數(shù)f（x）的單調(diào)性．
（2）設△OFG的面積S=
31
6
t，若O以為中心，F(xiàn)，為焦點的橢圓經(jīng)過點G，求當|
OG
|取最小值時橢圓的方程．
（3）在（2）的條件下，若點P的坐標為(0，
9
2
)，C，D是橢圓上的兩點，
PC
=λ
PD
(λ≠1)，求實數(shù)λ的取值范圍．

查看答案和解析>>

（2012年高考（浙江文））在△ABC中,內(nèi)角A,B,C的對邊分別為a,b,c,且bsinA=acosB.

(1)求角B的大小;

(2)若b=3,sinC=2sinA,求a,c的值.

查看答案和解析>>

在△ABC中,角A,B,C對應的邊分別是a,b,c.已知cos2A-3cos(B+C)=1.

(1)求角A的大小;

(2)若△ABC的面積S=5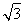,b=5,求sinBsinC的值.

 

查看答案和解析>>

（12分） 在中,      (1) 求角C的大小;     (2) 若最大邊長為,求最小邊長.

查看答案和解析>>


同步練習冊答案