
ν}ΡΩΝ–±μ(Αϋά®¥πΑΗΚΆΫβΈω)
| ïr(sh®Σ)ιgtΘ®ΧλΘ© | 1 | 3 | 6 | 10 | 36 | Γ≠ |
| »’δN έΝΩmΘ®ΦΰΘ© | 94 | 90 | 84 | 76 | 24 | Γ≠ |
| 1 |
| 4 |
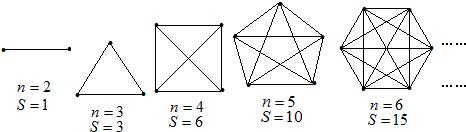
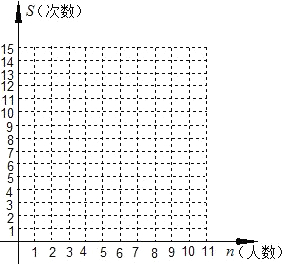
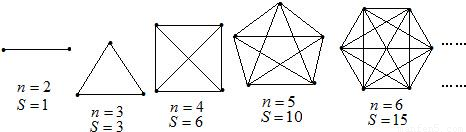


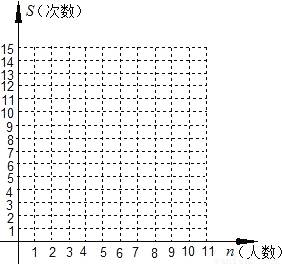
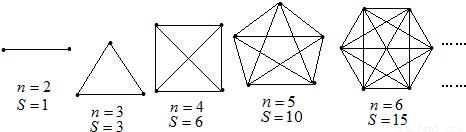

ΑΌΕ»÷¬–≈ - ΨöΝï(x®Σ)É‘(c®®)Ν–±μ - ‘΅ν}Ν–±μ
Κΰ±± ΓΜΞ¬™(li®Δn)ΨW(w®Θng)Ώ`Ζ®ΚΆ≤ΜΝΦ–≈œΔ≈eàσ(b®Λo)ΤΫ≈_(t®Δi) | ΨW(w®Θng)…œ”–ΚΠ–≈œΔ≈eàσ(b®Λo)¨ΘÖ^(q®±) | κä–≈‘pρ_≈eàσ(b®Λo)¨ΘÖ^(q®±) | …φöv ΖΧ™üo÷ςΝx”–ΚΠ–≈œΔ≈eàσ(b®Λo)¨ΘÖ^(q®±) | …φΤσ«÷ôύ(qu®Δn)≈eàσ(b®Λo)¨ΘÖ^(q®±)
Ώ`Ζ®ΚΆ≤ΜΝΦ–≈œΔ≈eàσ(b®Λo)κä‘£ΘΚ027-86699610 ≈eàσ(b®Λo)ύ]œδΘΚ58377363@163.com