
科目: 來源:第23章《二次函數(shù)與反比例函數(shù)》中考題集(23):23.5 二次函數(shù)的應(yīng)用(解析版) 題型:解答題

查看答案和解析>>
科目: 來源:第23章《二次函數(shù)與反比例函數(shù)》中考題集(23):23.5 二次函數(shù)的應(yīng)用(解析版) 題型:解答題
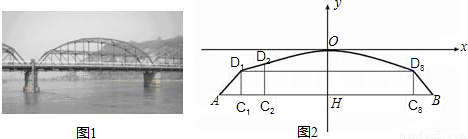
查看答案和解析>>
科目: 來源:第23章《二次函數(shù)與反比例函數(shù)》中考題集(23):23.5 二次函數(shù)的應(yīng)用(解析版) 題型:解答題
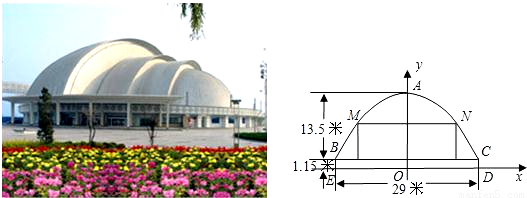
查看答案和解析>>
科目: 來源:第23章《二次函數(shù)與反比例函數(shù)》中考題集(23):23.5 二次函數(shù)的應(yīng)用(解析版) 題型:解答題

查看答案和解析>>
科目: 來源:第23章《二次函數(shù)與反比例函數(shù)》中考題集(23):23.5 二次函數(shù)的應(yīng)用(解析版) 題型:解答題
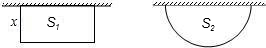
查看答案和解析>>
科目: 來源:第23章《二次函數(shù)與反比例函數(shù)》中考題集(23):23.5 二次函數(shù)的應(yīng)用(解析版) 題型:解答題
| 時間t(秒) | 50 | 100 | 150 | 200 | |
| 速度υ(米/秒) | 30 | 60 | 90 | 120 | |
| 路程x(米) | 750 | 3000 | 6750 | 12000 |
查看答案和解析>>
科目: 來源:第23章《二次函數(shù)與反比例函數(shù)》中考題集(23):23.5 二次函數(shù)的應(yīng)用(解析版) 題型:解答題
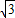 ≈1.732)
≈1.732)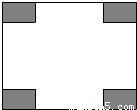
查看答案和解析>>
科目: 來源:第23章《二次函數(shù)與反比例函數(shù)》中考題集(23):23.5 二次函數(shù)的應(yīng)用(解析版) 題型:解答題
查看答案和解析>>
科目: 來源:第23章《二次函數(shù)與反比例函數(shù)》中考題集(23):23.5 二次函數(shù)的應(yīng)用(解析版) 題型:解答題
查看答案和解析>>
科目: 來源:第23章《二次函數(shù)與反比例函數(shù)》中考題集(23):23.5 二次函數(shù)的應(yīng)用(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com